Học đạo hàm để làm gì ?
Có khi nào bạn tự hỏi học đạo hàm ngoài việc để thi cử thì còn để làm gì ? Nếu bạn chỉ là một bác thợ xây bạn có cần biết đến đạo hàm không ? hay đạo hàm chỉ dành cho các nhà toán học ? Trung tâm luyện thi đại học đa minh xin gửi đến các bạn học sinh một bài viết nhỏ về ứng dụng của đạo hàm trong cuộc sống.
Xét từ nghĩa Hán việt của từ Đạo Hàm:
Đạo nghĩa là đường đi, hướng đi
Hàm nghĩa là hàm số
Đạo Hàm , hiểu nôm na là hướng đi của hàm số.
Xét từ định nghĩa toán học của đạo hàm:
(Bạn đọc có thể bỏ qua cho đỡ nhức đầu )
Tại một điểm x, hàm có giá trị là f(x). Xét một điểm gần đó x+a, hàm có giá trị f(x+a). Ta thấy x thay đổi một lượng là a, hàm thay đổi giá trị d=(f(x+a)-f(x). Giới hạn của thương số d/a khi a tiến đến 0 chính là đạo hàm. Rất là khó hiểu.
Ta thấy thế này, nếu đạo hàm, tức thương số d/a càng lớn thì chứng tỏ với một thay đổi nhỏ của x thì f(x) càng thay đổi nhiều, nghĩa là đạo hàm mang ý nghĩa về tốc độ biến đổi của hàm.
ví dụ nhé
– Nếu giá trị của đạo hàm tại x là >0, chứng tỏ rằng tại đó hàm số tăng theo x, hàm số đang đi lên
– Nếu giá trị của đạo hàm tại x là <0, chứng tỏ rằng tại đó hàm số giảm theo x, hàm số đang đi xuống
– Nếu giá trị của đạo hàm tại x là =0, chứng tỏ rằng tại đó hàm số không tăng cũng không giảm, hàm số đi ngang
Vậy, kết luận một cách hình tượng:
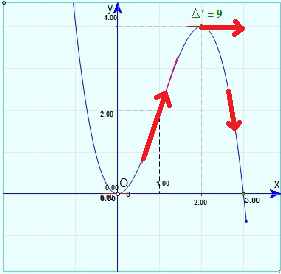
Nếu coi hàm số là con đường thì đạo hàm là mũi tên chỉ đường theo quy luật: bằng 0 là chỉ ngang, là đi ngang. Chỉ lên (>0) là hàm số đang tăng, chỉ xuống (<0) là hàm số đang giảm. Giá trị càng cao, hàm số biến đổi càng mạnh, mũi tên chỉ đường càng dốc.
Tại các điểm hàm số cực đại, nó không thể tăng thêm được nữa nên hàm số cũng bằng 0
Tại các điểm hàm số cực tiểu cũng vậy.
Ta cùng xét ứng dụng của nó nhé:
Chiếc máy tính đạo hàm trong nhà tôi: đồng hồ công-tơ-mét xe máy:
Ta không lạ, trên xe máy có cái đồng hồ công tơ mét này:

lúc x =10 giờ khởi hành, công tơ mét chỉ quãng đường xe đã đi trước đó là f(x) = 30025 km, lúc x= 10 giờ + 6 phút , công tơ mét chỉ f(x+a) = 30029 km. quãng đường đi được (fx+a)-f(x) = 4km, trong thời gian a=6 phút hay 1/10 giờ. Vậy tôi đang đi tốc độ là [(fx+a)-f(x)]/a = 40km/giờ. Vậy ta thấy rằng, kim tốc độ sẽ chỉ ở 40km/giờ phải không nào ?
Hóa ra chiếc kim tốc độ chính là chiếc máy tính đạo hàm con đường tôi đi được theo thời gian không biết mệt mỏi. Khi tôi dừng lại, ồ, kim chỉ số 0 ! tức là quãng đường không tăng không giảm, tức là tôi đứng yên !
Vận động viên chạy và bơi phối hợp:
Giả thiết thế này nhé, có một cái hồ rộng 50m, dài 200m. Một vật động viên chạy phối hợp với bơi (bắt buộc cả hai) cần đi từ góc này qua góc đối diện bằng cách cả chạy và bơi (đường mầu đỏ) như hình vẽ. Hỏi rằng sau khi chạy được bao xa (quãng đường x) thì nên nhảy xuống bơi để đến đích nhanh nhất ? biết rằng vận tốc bơi là 1.5 m/s , vận tốc chạy là 4.5m/s.
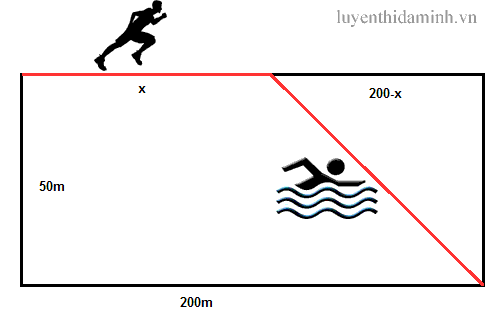
thời gian chạy: x/4
quãng đường để bơi là chiều dài đường chéo tam giác vuông có cạnh 200-x và 50, từ đó tính được thời gian bơi.
Tổng hai thời gian là hàm số của x.
Để tìm ra thời gian cực tiểu, khi đó rõ ràng đạo hàm của nó theo x phải bằng 0. Các bạn tự giải bài cực trị này nhé
Bài toán cực tiểu của Bác Thợ Xây
Bạn muốn xây dựng một bình chứa nước hình trụ thể tích 150 m^3. Đáy bằng bê tông giá 100.000 VND /m^2, thành bằng tôn, giá 90.000 VND /m^2, bề mặt bằng nhôm không han giá 120.000 VND/m^2. Vậy kích thước của bình chứa nước như thế nào để số tiền xây dựng nó là ít nhất ?
Bài này rất quen thuộc phải không ? Công việc của mấy bác thợ xây cũng như vậy đó. Họ thiết kế sao cho chi phí là thấp nhất.
Bài bày chúng tôi không gợi ý giải, liệu các bạn có giúp được bác thợ xây không ?




